Main Sim Manager for the fluctuating fluid simulation
Provide a class (properties and methods) for the simulations of a particle passively advecting by a fluctuation fluid described by a generalized Rouse kernel. No coupling between fluid and particle. Follows the description of the JCP paper. Additionally provides a series of methods for doing one point microrheology on the generated data.
Contents
- Properties
- Method: Initialize the sim
- Method: Delete the sim and his content (necesary)
- Method: Generate physical parameters
- Method: Generate the sinc function for integration
- Method: Generate and write to disk the Cholesky of the covariance
- Method: Build the covariance matrix and find its Cholesky.
- Method: Generate integral increment.
- Method: Generate and write path
- Method: Find MSD
- Method: Find Increment ACF
- Method: Read the Cholskey decomposition of the covariance matrix
- Method: Read already generated path (bin)
- Method: Create filename
- The end
Based on the non-dimensional equations for the fluid and the particle.
Include read and write methods for data saved to output folder.
Christel Hohenegger
Last updated: 07/15/2016
classdef SimManager < handle
Properties
- Physical parameters:
- Number of particles, initial positions: passed onto the sim.
- Covariance matrix: contains all three for the off and on diagonal terms.
- Integral increment for the particle update: contains all on and off diagonal increments for both u and v.
- Particle paths: x and y.
- Mean square displacement (MSD): x and y.
- Increment auto-correlation (ACF): x and y.
- Output directory and file name.
- Helper functions for the evaluation of the integral.
properties
parameters;
dataCov;
dataIncND;
dataPathND = [];
dataMSDND;
dataIncACFND;
outputDir = './SimManagerOutput';
dataFullFn = [];
sinc2Array = {[]};
xsiSincVal = {[]};
PhiRealSincVal = {[]};
PhiImagSincVal = {[]};
end
methods
Method: Initialize the sim
Input: (output directory) Create the name of the .mat file containing important info
function obj = SimManager(outputDir) if exist('outputDir', 'var') obj.outputDir = outputDir; end if isempty(obj.outputDir) obj.outputDir = uigetdir; end if isempty(dir(obj.outputDir)) mkdir(obj.outputDir); elseif ~isdir(obj.outputDir) error([obj.outputDir,' exists, but is not a directory. ']) end obj.SetFileName; end
Method: Delete the sim and his content (necesary)
function delete(~) end
Method: Generate physical parameters
Generate a set of default parameters
Units: [time]=ms, [length]=microns, [mass]=mg.
- Boltzman constant times temperature: microns^2*mg/ms^2
- Solvent density: water mg/microns^3
- Solvent dynamic viscosity: water mg/microns/time
- Particle's radius: microns
- G0: mean polymer stress (fixed)
- Smallest relaxation time: ms
- Time step, number of time steps, final time, number of paths
- Length of the domain: microns
- Number of Fourier modes
- Rouse exponent
- Number of particles and initial positions
- Relaxation times: given as Generalized Rouse spectrum
- Average relaxation time
- Polymer dynamic viscosity: given as the mean polymer stress divided by the average relaxation time
- Solvent and polymer kinematic viscosity
Non dimensional groups:
 : characteristic time
: characteristic time : nondimensional parameter for particle
: nondimensional parameter for particle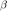 : nondimensional parameter for fluid
: nondimensional parameter for fluid- U: characteristic velocity
- Reynolds number
- Necessary nondimensional times and lengths
function GenerateParameters(obj) % Dimensional basic parameters obj.parameters.kbt = 4.1e-9; obj.parameters.rho = 1e-9; obj.parameters.etasol = 1e-6; obj.parameters.radius = 1; obj.parameters.numKernels = 1e0; obj.parameters.G0 = 1e-4; obj.parameters.tau0 = 1; obj.parameters.dt = 1; obj.parameters.numTsteps = 2^10; obj.parameters.tFinal = obj.parameters.numTsteps*obj.parameters.dt; obj.parameters.numPaths = 1e3; obj.parameters.length = 10; obj.parameters.numFmodes = 16; obj.parameters.alpha = 2; obj.parameters.numParticles = 1; obj.parameters.inX = obj.parameters.length/2; obj.parameters.inY = obj.parameters.length/2; % Derived dimensional basic parameters obj.parameters.tau = obj.parameters.tau0*(obj.parameters.numKernels... ./(obj.parameters.numKernels-(0:obj.parameters.numKernels-1)))... .^(obj.parameters.alpha); obj.parameters.tauavg = 1/obj.parameters.numKernels... *sum(obj.parameters.tau); obj.parameters.etapol = obj.parameters.G0*obj.parameters.tauavg; obj.parameters.nusol = obj.parameters.etasol/obj.parameters.rho; obj.parameters.nupol = obj.parameters.etapol/obj.parameters.rho; % ND groups and parameters obj.parameters.theta = obj.parameters.length^2/obj.parameters.nusol; obj.parameters.tauND = obj.parameters.tau/obj.parameters.theta; obj.parameters.tauavgND = obj.parameters.tauavg/obj.parameters.theta; obj.parameters.dtND = obj.parameters.dt/obj.parameters.theta; obj.parameters.kappa = sqrt(obj.parameters.kbt*obj.parameters.rho)... /obj.parameters.etasol; obj.parameters.beta = obj.parameters.nupol*obj.parameters.length^2 ... /(obj.parameters.nusol^2*obj.parameters.tauavg); obj.parameters.U = sqrt(obj.parameters.kbt/obj.parameters.rho... /obj.parameters.length^3); obj.parameters.lengthND = obj.parameters.length/obj.parameters.length; obj.parameters.radiusND = obj.parameters.radius/obj.parameters.length; obj.parameters.Reynolds = obj.parameters.U*obj.parameters.length... /obj.parameters.nusol; obj.parameters.inXND = obj.parameters.inX/obj.parameters.length; obj.parameters.inYND = obj.parameters.inY/obj.parameters.length; end
Method: Generate the sinc function for integration
Not saved to a file. Needed to compute the covariance matrix. Follows the definition of the JCP paper. Requires the sinc package.
The sinc part of the integral is defined as a sincfun. For every time, it is the square of a sinc function. Then the sincpoints are extracted and PhiRel and PhiImag are evaluated at these points. All are necessary to build rhohat and the integrand.
Warning: domain is preset to [0,100].
function GenSincFun(obj) timeND = obj.parameters.dtND*(0:obj.parameters.numTsteps); numKernels = obj.parameters.numKernels; tauND = obj.parameters.tauND; lambdaND = 1./tauND; PhiRealFun = @(x) arrayfun(@(z) 1/numKernels*... sum(lambdaND./(z.^2+lambdaND.^2)),x); PhiImagFun = @(y) arrayfun(@(z) 1/numKernels*... sum(-z./(z.^2+lambdaND.^2)),y); sincfunpref('domain',[0,1e2]); for tindex = 2:length(timeND) sinc2Fun = @(z) (sin(z*timeND(tindex)/2)./z).^2; obj.sinc2Array{tindex} = sincfun(sinc2Fun); obj.xsiSincVal{tindex} = sincpts(obj.sinc2Array{tindex}); obj.PhiRealSincVal{tindex} = PhiRealFun(obj.xsiSincVal{tindex}); obj.PhiImagSincVal{tindex} = PhiImagFun(obj.xsiSincVal{tindex}); end end
Method: Generate and write to disk the Cholesky of the covariance
Requires the initialized sinc functions. Integral is evaluated at the sinc points defined elsewhere. Compute the j integral at each time for the on and off term. Requires building rhohat and the integrand at the sinc points. Integration is done with trapz.
Requires the additional method function CovMat to build the Cholesky decomposition of the matrix given the j values.
function GenWriteCovMat(obj) if exist(obj.dataFullFn,'file') error('Output file exists') end [fp,fn,fe] = fileparts(obj.dataFullFn); numFmodes = obj.parameters.numFmodes; numTsteps = obj.parameters.numTsteps; timeND = obj.parameters.dtND*(0:obj.parameters.numTsteps); % Wave numbers in x and y kx = 0:numFmodes-1; ky = 0:numFmodes-1; [kxx,kyy] = ndgrid(kx,ky); % Magnitude of the wave vector kkMat = zeros(numFmodes,numFmodes); for iindex=1:numFmodes for jindex=1:numFmodes kkMat(iindex,jindex)=sqrt(kxx(iindex,jindex).^2+... kyy(iindex,jindex).^2); end end count = 1; % Linear vector of the magnitude matrix kVec = NaN(numFmodes^2/2,1); for iindex=1:numFmodes for jindex =1:iindex if iindex==1 && jindex ==1 continue end kVec(count) = kkMat(iindex,jindex); count = count+1; end end tic1=tic; matC = zeros(numTsteps,numTsteps,2); jDiagValSinc = NaN(length(kVec),length(timeND)); jOffDiagValSinc = NaN(length(kVec),length(timeND)); cDiag = 1/(2*pi); cOffDiag = 1/(2*pi*sqrt(2)); beta = obj.parameters.beta; % Integral depends on k for iindex = 1:length(kVec) % Build the integrand at every time, integrate with trapz for tindex = 2:length(timeND) rhoHatSincVal = 2*1/kVec(iindex)^2*(1+... beta*obj.PhiRealSincVal{tindex})... ./((1+beta*obj.PhiRealSincVal{tindex}).^2 ... +(obj.xsiSincVal{tindex}/kVec(iindex)^2+... beta*obj.PhiImagSincVal{tindex}).^2); integrand = rhoHatSincVal.*... sincvals(obj.sinc2Array{tindex}); jtemp = trapz(obj.xsiSincVal{tindex},integrand); jDiagValSinc(tindex) = cDiag^2*2/pi*jtemp; jOffDiagValSinc(tindex) = cOffDiag^2*2/pi*jtemp; end jDiagValSinc(1) = 0; jOffDiagValSinc(1) = 0; % Find the Cholesky matC(:,:,1) = obj.CovMat(obj,jDiagValSinc); matC(:,:,2) = obj.CovMat(obj,jOffDiagValSinc); % Write to disk fn1 = fullfile(fp,[fn,'_k', num2str(iindex),... '_CholCovDiag',fe]); fn2 = fullfile(fp,[fn,'_k', num2str(iindex),... '_CholCovOffDiag',fe]); fid1 = fopen(fn1,'w','a'); fid2 = fopen(fn2,'w','a'); fwrite(fid1,matC(:,:,1),'float64','a'); fwrite(fid2,matC(:,:,2),'float64','a'); fclose(fid1); fclose(fid2); end toc1=toc(tic1); fprintf(... 'Time to generate the covariance matrix for all k: %d s.\n',... round(toc1)) end
Method: Build the covariance matrix and find its Cholesky.
Uses block form for speed up. Catch error due to numerical error in the integration resulting in negative eigenvalues. If that's the case, decompose the matrix, replace the appropriate entries in the diagonal matrix and rebuild the matrix. Return the Cholesky in full form (not block).
function matC=CovMat(obj,jInt) numTsteps = obj.parameters.numTsteps; numBlocks = min(2^10,numTsteps); count = numTsteps/numBlocks; matA = zeros(numBlocks,numBlocks,count,count); jVal = zeros(numBlocks+1,count); % Transform the j values to block form for iindex=1:count jVal(:,iindex) = jInt(1+(iindex-1)*numBlocks:... 1+iindex*numBlocks); end % Build the covariance. Uses Toeplitz structure. for iindex=1:count for jindex=1:iindex matR3 = repmat(jVal(2:end,jindex)',numBlocks,1); matR1 = repmat(jVal(2:end,iindex),1,numBlocks); if iindex==jindex matR2 = toeplitz(jVal(1:end-1,1)); else matR2 = toeplitz(jVal(1:end-1,iindex-jindex+1),... flipud(jVal(2:end,iindex-jindex))'); end matA(:,:,iindex,jindex) = matR1-matR2+matR3; end end % Find the Cholesky. Fixes negative EV matL = zeros(numBlocks,numBlocks,count,count); tol = 1e-8; for iindex=1:count for jindex=1:iindex if iindex==jindex temp = 0; for kindex=1:iindex-1 temp = temp+squeeze(matL(:,:,iindex,kindex))... *squeeze(matL(:,:,iindex,kindex))'; end try matL(:,:,iindex,jindex) = chol(squeeze(... matA(:,:,iindex,jindex))-temp,'lower'); catch [matV,matD]=eig(squeeze(matA(:,:,iindex,jindex))... -temp,'nobalance'); diag(matD); vecD = diag(matD); fprintf('ERROR: Matrix is not positive definite.\n') fprintf('Largest negative EV %6.4e .\n',min(vecD)) vecD(vecD<0)=tol; matC = matV*diag(vecD)/matV; matL(:,:,iindex,jindex) = chol(matC,'lower'); end else temp = 0; for kindex=1:jindex-1 temp = temp+squeeze(matL(:,:,iindex,kindex))... *squeeze(matL(:,:,jindex,kindex))'; end matL(:,:,iindex,jindex) = (squeeze(matA(:,:,... iindex,jindex))-temp)/(squeeze(matL(:,:,... jindex,jindex))'); end end end % Rebuild the matrix matC = zeros(numTsteps,numTsteps); for iindex=1:count for jindex=1:iindex matC(1+(iindex-1)*numBlocks:iindex*numBlocks,... 1+(jindex-1)*numBlocks:jindex*numBlocks) = ... matL(:,:,iindex,jindex); end end end
Method: Generate integral increment.
Needed to update the paths. Not saved to disk. Requires the Cholesky of the covariance matrix calculated elsewhere.
Covariance algorithm: multiply the Cholesky of the covariance matrix by a unit random normal vector.
Even though only half+diagonal matrices are saved because of symmetry, for the increment we need all of them, hence the if statement. The only difference is that the randn vector is different. Print all the increments to the object using linear index count.
function GenIntegralInc(obj) numTsteps = obj.parameters.numTsteps; numFmodes = obj.parameters.numFmodes; count = 1; for iindex=1:numFmodes for jindex=1:iindex if iindex==1 && jindex ==1 continue end dummy = sub2ind([numFmodes,numFmodes],iindex,jindex); dummy2 = sub2ind([numFmodes,numFmodes],jindex,iindex); matC1 = obj.dataCov(count).matCholCovDiag; matC2 = obj.dataCov(count).matCholCovOffDiag; zeta11 = matC1*randn(numTsteps,1); zeta22 = matC1*randn(numTsteps,1); zeta12 = matC2*randn(numTsteps,1); zetaInc11(1) = zeta11(1); zetaInc11(2:numTsteps) = diff(zeta11,1); zetaInc12(1) = zeta12(1); zetaInc12(2:numTsteps) = diff(zeta12,1); zetaInc22(1) = zeta22(1); zetaInc22(2:numTsteps) = diff(zeta22,1); obj.dataIncND(dummy).zetaInc11 = zetaInc11; obj.dataIncND(dummy).zetaInc12 = zetaInc12; obj.dataIncND(dummy).zetaInc22 = zetaInc22; if jindex ~= iindex zeta11 = matC1*randn(numTsteps,1); zeta22 = matC1*randn(numTsteps,1); zeta12 = matC2*randn(numTsteps,1); zetaInc11(1) = zeta11(1); zetaInc11(2:numTsteps) = diff(zeta11,1); zetaInc12(1) = zeta12(1); zetaInc12(2:numTsteps) = diff(zeta12,1); zetaInc22(1) = zeta22(1); zetaInc22(2:numTsteps) = diff(zeta22,1); obj.dataIncND(dummy2).zetaInc11 = zetaInc11; obj.dataIncND(dummy2).zetaInc12 = zetaInc12; obj.dataIncND(dummy2).zetaInc22 = zetaInc22; end xi11 = matC1*randn(numTsteps,1); xi22 = matC1*randn(numTsteps,1); xi12 = matC2*randn(numTsteps,1); xiInc11(1) = xi11(1); xiInc11(2:numTsteps) = diff(xi11,1); xiInc12(1) = xi12(1); xiInc12(2:numTsteps) = diff(xi12,1); xiInc22(1) = xi22(1); xiInc22(2:numTsteps) = diff(xi22,1); obj.dataIncND(dummy).xiInc11 = xiInc11; obj.dataIncND(dummy).xiInc12 = xiInc12; obj.dataIncND(dummy).xiInc22 = xiInc22; if jindex ~= iindex xi11 = matC1*randn(numTsteps,1); xi22 = matC1*randn(numTsteps,1); xi12 = matC2*randn(numTsteps,1); xiInc11(1) = xi11(1); xiInc11(2:numTsteps) = diff(xi11,1); xiInc12(1) = xi12(1); xiInc12(2:numTsteps) = diff(xi12,1); xiInc22(1) = xi22(1); xiInc22(2:numTsteps) = diff(xi22,1); obj.dataIncND(dummy2).xiInc11 = xiInc11; obj.dataIncND(dummy2).xiInc12 = xiInc12; obj.dataIncND(dummy2).xiInc22 = xiInc22; end count = count+1; end end end
Method: Generate and write path
Save path to bin file. 100 Paths are saved in the same bin. Each path has length number of time step+1 times number of particles. Requires the index of path. Loop over all paths is outside.
Semi-Euler step in time (loop of number of time steps).
Requires the velocity integral increment from the fluids u and v generated elsewhere (not saved to disk).
function GenWritePath(obj,pathNdx) [fp,fn,fe] = fileparts(obj.dataFullFn); numParticles = obj.parameters.numParticles; numTsteps = obj.parameters.numTsteps; radiusND = obj.parameters.radiusND; numFmodes = obj.parameters.numFmodes; kappa = obj.parameters.kappa; % Wave numbers in x and y kx = 0:numFmodes-1; ky = 0:numFmodes-1; [kxx,kyy] = ndgrid(kx,ky); % Magnitude of the wave vector kk = zeros(numFmodes,numFmodes); for iindex=1:numFmodes for jindex=1:numFmodes kk(iindex,jindex)=sqrt(kxx(iindex,jindex).^2+... kyy(iindex,jindex).^2); end end % Fourier transform of the blob phihat = exp(-kk.^2*radiusND^2/2); % Projection matrix, remove the NaN in the first entry p11 = ones(size(kxx))-kxx.*kxx./kk.^2; p12 = -kxx.*kyy./kk.^2; p21 = -kyy.*kxx./kk.^2; p22 = ones(size(kxx))-kyy.*kyy./kk.^2; p11(1,1) = 1; p12(1,1) = 0; p21(1,1) = 0; p22(1,1) = 1; tic xPathND = zeros(numTsteps+1,numParticles); yPathND = zeros(numTsteps+1,numParticles); xPathND(1,:) = obj.parameters.inXND; yPathND(1,:) = obj.parameters.inYND; for nindex=1:numTsteps % Construct the velocity integral increments both for u and % v (3 each, symmetric). Skip the zeroth wave vector. % Convert the (kx,ky) vector to the dummy linear index. zetaInc11 = zeros(numFmodes,numFmodes); zetaInc12 = zeros(numFmodes,numFmodes); zetaInc22 = zeros(numFmodes,numFmodes); xiInc11 = zeros(numFmodes,numFmodes); xiInc12 = zeros(numFmodes,numFmodes); xiInc22 = zeros(numFmodes,numFmodes); for dummy=1:numFmodes^2 [iindex,jindex] = ind2sub([numFmodes,numFmodes],dummy); if iindex==1 && jindex ==1 continue else zetaInc11(iindex,jindex) = ... obj.dataIncND(dummy).zetaInc11(nindex); zetaInc12(iindex,jindex) = ... obj.dataIncND(dummy).zetaInc12(nindex); zetaInc22(iindex,jindex) = ... obj.dataIncND(dummy).zetaInc22(nindex); xiInc11(iindex,jindex) = ... obj.dataIncND(dummy).xiInc11(nindex); xiInc12(iindex,jindex) = ... obj.dataIncND(dummy).xiInc12(nindex); xiInc22(iindex,jindex) = ... obj.dataIncND(dummy).xiInc22(nindex); end end kkInv = kk.^(-1); kkInv(1,1) = 0; % Path update (expanded version) for iindex = 1:numParticles xPathND(nindex+1,iindex) = xPathND(nindex,iindex)... +2*kappa*sum(sum(phihat.*kkInv... .*(cos(kxx*xPathND(nindex,iindex)... +kyy*yPathND(nindex,iindex))... .*(p11.*(zetaInc11.*kxx+zetaInc12.*kyy)... +p12.*(zetaInc12.*kxx+zetaInc22.*kyy))... -sin(kxx*xPathND(nindex,iindex)... +kyy*yPathND(nindex,iindex))... .*(p11.*(xiInc11.*kxx+xiInc12.*kyy)... +p12.*(xiInc12.*kxx+xiInc22.*kyy))))); yPathND(nindex+1,iindex) = yPathND(nindex,iindex)... +2*kappa*sum(sum(phihat.*kkInv... .*(cos(kxx*xPathND(nindex,iindex)... +kyy*yPathND(nindex,iindex))... .*(p21.*(zetaInc11.*kxx+zetaInc12.*kyy)... +p22.*(zetaInc12.*kxx+zetaInc22.*kyy))... -sin(kxx*xPathND(nindex,iindex)... +kyy*yPathND(nindex,iindex))... .*(p21.*(xiInc11.*kxx+xiInc12.*kyy)... +p22.*(xiInc12.*kxx+xiInc22.*kyy))))); end end endtime=toc; if mod(pathNdx,100)==0 fprintf('Time to generate one path %6.4f\n',endtime) end % Write path to a file (100 at a time). teilNdx = floor((pathNdx-1)/100)+1; fn1 = fullfile(fp,[fn,'_',sprintf('%3.3d',numParticles),... 'Part_xPos_Teil',sprintf('%3.3d',teilNdx),fe]); fn2 = fullfile(fp,[fn,'_',sprintf('%3.3d',numParticles),... 'Part_yPos_Teil',sprintf('%3.3d',teilNdx),fe]); fid1 = fopen(fn1,'a','a'); fid2 = fopen(fn2,'a','a'); fwrite(fid1,xPathND,'float64',0,'a'); fwrite(fid2,yPathND,'float64',0,'a'); fclose(fid1); fclose(fid2); end
Method: Find MSD
function FindMSD(obj) numParticles = obj.parameters.numParticles; numTsteps = obj.parameters.numTsteps; numPaths = obj.parameters.numPaths; xSDND = zeros(numTsteps+1,numPaths,numParticles); ySDND = zeros(numTsteps+1,numPaths,numParticles); for iindex=1:numPaths xSDND(:,iindex,:) = (obj.dataPathND.x(:,:,iindex)-... repmat(obj.dataPathND.x(1,:,iindex),numTsteps+1,1)).^2; ySDND(:,iindex,:) = (obj.dataPathND.y(:,:,iindex)-... repmat(obj.dataPathND.y(1,:,iindex),numTsteps+1,1)).^2; end obj.dataMSDND.x = squeeze(mean(xSDND,2)); obj.dataMSDND.y = squeeze(mean(ySDND,2)); end
Method: Find Increment ACF
Uses acf code.
Additional inputs: separation (lag time) and number of ACF time steps. Needed if data are generated with different time steps.
function FindIncACF(obj,sep,numTACF) numPaths = obj.parameters.numPaths; xACFND = zeros(numTACF-1,numPaths); yACFND = zeros(numTACF-1,numPaths); for jindex=1:numPaths xPathND = obj.dataPathND.x(1:sep:end,:,jindex); yPathND = obj.dataPathND.y(1:sep:end,:,jindex); xACFtemp = acf(diff(xPathND),0:numTACF-2); yACFtemp = acf(diff(yPathND),0:numTACF-2); xACFND(:,jindex)=xACFtemp; yACFND(:,jindex)=yACFtemp; end obj.dataIncACFND.x = squeeze(mean(xACFND,2)); obj.dataIncACFND.y = squeeze(mean(yACFND,2)); end
Method: Read the Cholskey decomposition of the covariance matrix
On and off diagonal matrix. Matrices are numbered based on the linear index (called dummy) corresponding to the values of (kx,kl). Only need half plus the diagonal. Each matrix is of size number of time steps times number of time steps.
function ReadCholCov(obj) numTsteps = obj.parameters.numTsteps; numFmodes = obj.parameters.numFmodes; [fp,fn,fe] = fileparts(obj.dataFullFn); for dummy=1:(numFmodes*(numFmodes+1)/2-1) fn1 = fullfile(fp,[fn,'_k', num2str(dummy),... '_CholCovDiag',fe]); fn2 = fullfile(fp,[fn,'_k', num2str(dummy),... '_CholCovOffDiag',fe]); fid1 = fopen(fn1,'r','a'); fid2 = fopen(fn2,'r','a'); obj.dataCov(dummy).matCholCovDiag = fread(fid1,... [numTsteps,numTsteps],'float64','a'); obj.dataCov(dummy).matCholCovOffDiag = fread(fid2,... [numTsteps,numTsteps],'float64','a'); fclose(fid1); fclose(fid2); end end
Method: Read already generated path (bin)
To save memory 100 paths are saved in the bin file. The paths are read and reformated as a big array of size number of time steps +1 times number of particles times number of paths
function ReadPath(obj) numParticles = obj.parameters.numParticles; numTsteps = obj.parameters.numTsteps; numPaths = obj.parameters.numPaths; [fp,fn,fe] = fileparts(obj.dataFullFn); for jj=1:floor(numPaths/100) fn1 = fullfile(fp,[fn,'_',sprintf('%3.3d',numParticles),... 'Part_xPos_Teil',sprintf('%3.3d',jj),fe]); fn2 = fullfile(fp,[fn,'_',sprintf('%3.3d',numParticles),... 'Part_yPos_Teil',sprintf('%3.3d',jj),fe]); fid1 = fopen(fn1,'r','a'); fid2 = fopen(fn2,'r','a'); temp = fread(fid1,[(numTsteps+1)*numParticles,100],... 'float64','a'); xPath(:,:,1+(jj-1)*100:100*jj) = ... reshape(temp,[(numTsteps+1),numParticles,100]); temp = fread(fid2,[(numTsteps+1)*numParticles,100],... 'float64','a'); yPath(:,:,1+(jj-1)*100:100*jj) = ... reshape(temp,[(numTsteps+1),numParticles,100]); fclose(fid1); fclose(fid2); end obj.dataPathND.x = xPath; obj.dataPathND.y = yPath; end
Method: Create filename
Create a new filename if the parameters set are different than what already exist, otherwise load the file.
function SetFileName(obj) datFileNdxFn = fullfile(obj.outputDir, 'datFileNdx.mat'); if exist(datFileNdxFn, 'file') ext = load(datFileNdxFn); fileNdx = ext.fileNdx; else fileNdx = []; end for iindex = 1:length(fileNdx) if isequal(fileNdx(iindex), obj.parameters) obj.dataFullFn = fullfile( obj.outputDir, [ ... 'dataSet_', sprintf('%3.3d', iindex), '.bin']); break; end end if isempty(obj.dataFullFn) fileNdx = [fileNdx; obj.parameters]; obj.dataFullFn = fullfile( obj.outputDir, [ ... 'dataSet_', sprintf('%3.3d', length(fileNdx)),... '.bin']); end save(datFileNdxFn,'fileNdx'); end
The end
end
end