Research

My current research interests are:

• Active cloaking and mimicking for the wave, heat equations and related phenomena.
• Network based inversion methods for elliptic equations (electrical impedance tomography, aquifer imaging, elasticity, Schrödinger equation, ...).
• Optics, hyperspectral imaging.
• Manipulation of small particles using acoustic fields.
• Imaging with waves: interferometric methods and electromagnetic waves.

For more details, here is a list of publications and my resume.

For a few research highlights see: active exterior cloaking and the manipulation of small particles using sound.

Active exterior cloaking

Active sources can be used to cloak objects from probing "fields"¹. I am using "field" very broadly here as we were successful in using this approach for currents in a conductive plate³ (Laplace equation), for waves⁴⁵⁶ (Helmholtz equation),the heat equation ¹¹¹² and for random walks in graphs ¹³. Others have applied the same principle to waves propagating in thin plates ⁷⁹ and elasticity ⁸ or even provided explicit formulas for the series expansions involved ¹⁰. This approach has the following advantages:

• custom made materials with exotic properties are not required
• cloaking over a broad band of frequencies is possible
• mimicking an object (i.e. making an orange look like an apple) is possible with relatively minor modifications².

For an illustration with waves see the video below.

The principle behind this cloaking method is the same as that of noise cancelling headphones. We design active devices that are tailored to cancel the incoming wave in some region without revealing their position from far away. Thus any object inside this region will be invisible, regardless of its shape. Our devices appear in the simulations on the left or the still images below. Here is a possible scenario to explain what is happening in the simulations. Imagine that the traveling wave is a radar pulse and that "kite" is a plane. When the devices are inactive (left portion of animation), the radar pulse reflects on the kite and these reflections could be used to know the position of the kite. When the devices are active (right portion of animation), the devices cancel out the radar pulse in a region and then rebuilds it as if there was no kite. Thus the object is hidden from the radar. Although our simulations are purely two dimensional, the method works in three dimensions as well⁶.

One disadvantage of this active cloaking method is that one needs to know the incoming wave in advance. This could be achieved by having outpost sensors that relay this information to the devices. Therefore information from the sensors has to travel faster to the devices than the incoming wave. This is achievable if we are working with water waves or earthquakes. However for electromagnetic waves, the information cannot travel faster than light, and so our scheme would not be feasible, unless something is assumed about the incoming wave (for example that the radar pulse is periodic and that we have a couple of periods to become invisible).

We first proposed this method for "waves" with a very small frequency, which satisfy the so called Laplace equation. In this case only one device is needed. For an illustration see the simulations below. On the left the device would be inside the "black bean" and the region to be cloaked the small white circle to the right of the bean. The field lines of the probing field should be vertical. The presence of a small scatterer inside the white circle (left) deforms the field lines and means one can detect the presence of the scatterer. Now when the cloaking device is active (right), the field lines are for all practical purposes vertical, and so the object is invisible and cannot be detected. (Images from the article³)

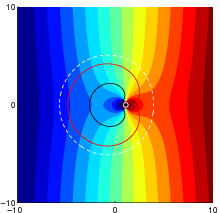
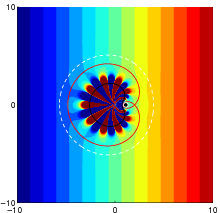
In our most recent work¹¹¹² we use active sources of heat to cloak objects from thermal measurements. This is illustrated below with a movie. On the left pane, we see a yellow blow propagating. This is the temperature in a plate resulting from heating the plate at the center of the blob at a certain time and then stopping the heat. Since the plate is made of the same material, the isotherms will be circles. On the middle pane, there is a Homer Simpson shaped object that is set (artificially) at the lowest temperature. Now the isotherms are not circles anymore, so it is possible to know that there is an object there since the isotherms are not circles anymore. In the right pane, the active cloak (the red crosses) creates a region that is at the same temperature as the object, all while keeping the isotherms as if there was nothing there, hence hiding the object. For those interested in the Mathematics behind this: this is an application of the Green identities to reproduce solutions to the heat equation inside or outside of a domain. Reproduction inside of a domain is well known, however for reproduction outside of a domain, we had to come up with growth conditions on solutions to the heat equation to guarantee that they can be reproduced using this method.

This is nice, however the object we want to hide is completely surrounded by special sources (red crosses above). Fortunately one can move sources on the active sources to a few locations. The final result is that these new special sources are sufficient to cloak an object. This is illustrated below: the left pane is the uncloaked configuration (a very localized heat source that fires at time zero and then is extinguished), the middle pane is the configuration with a kite object which is set to a zero temperature and the right pane shows the special sources. These look like urchins and although they are mathematically point sources, the temperature inside these urchins is extremely high. Of course, one replace each of these urchins by an active surface surrounding each of the urchins, still leaving gaps between the object and the exterior. Hence this is called "exterior" cloaking. From a mathematical perspective, the novelty is that we allow the wavenumber to be complex in the Helmholtz equation (which is the case when analyzing the heat equation in the "frequency" domain). The tool to move sources around is the Graf addition formula and we have derived convergence estimates for this series which allow us to quantify a priori the cloaking performance.

Collaborators: Daniel Onofrei (Mathematics, U of Houston) and I started working on this problem in 2008 with guidance and ideas by Graeme Milton (Mathematics, U of Utah). I did not work on this problem for a few years until I had a nice conversation with Sébastien Guenneau (UMI Abraham DeMoivre, CNRS) and Maxence Cassier (Institut Fresnel, Marseille, France) over coffee at the Fresnel Institute in 2017. I resumed working on this problem bringing Ph.D. student Trent DeGiovanni onboard. Trent is now a postdoc at Dartmouth.

Manipulation of small particles using sound

Acoustic waves in a liquid can displace small particles in suspension. When the particles are smaller than the wavelength, one can predict the end position of the particles fairly well by looking at the minima of the so-called acoustic radiation potential. I have a long-standing collaboration with Bart Raeymaekers (Mechanical Engineering, Virginia Tech formerly at the U. of Utah) and his lab where we study different theoretical and experimental aspects of this problem. We discovered that the problem of placing particles at a particular point¹⁴ can be re-formulated as a simpler mathematical problem (namely finding a particular eigenvector for a Hermitian matrix). This idea permeates several developments in this area, including trapping high aspect ratio particles¹⁵ and studying the effect of viscosity¹⁶. In the case where the particles are neutrally buoyant and less compressible than the surrounding fluid, we have mathematically showed¹⁷ that it is possible to place particles in rather arbitrary arrangements in a plane if we can control waves from arbitrary directions in three dimensions. The idea is to embed the desired particle positions in the level-set of a function and then approximate the function using waves. As an example, we have a desired U pattern below in black and with this procedure we are guaranteed that the particles will cluster around the red curve. You may notice that the red curve is not exactly like the black one. This is because the approximation is limited by roughly a wavelength. Physically speaking this is due to us assuming that the waves are controlled from the far field, which leads to the approximation being done with band-limited functions.

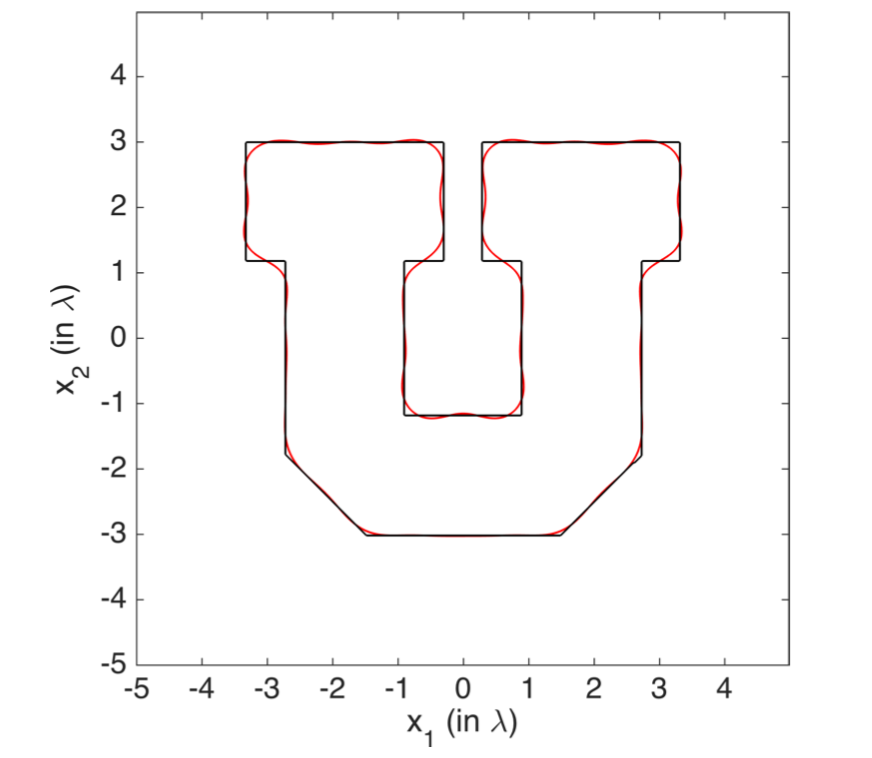
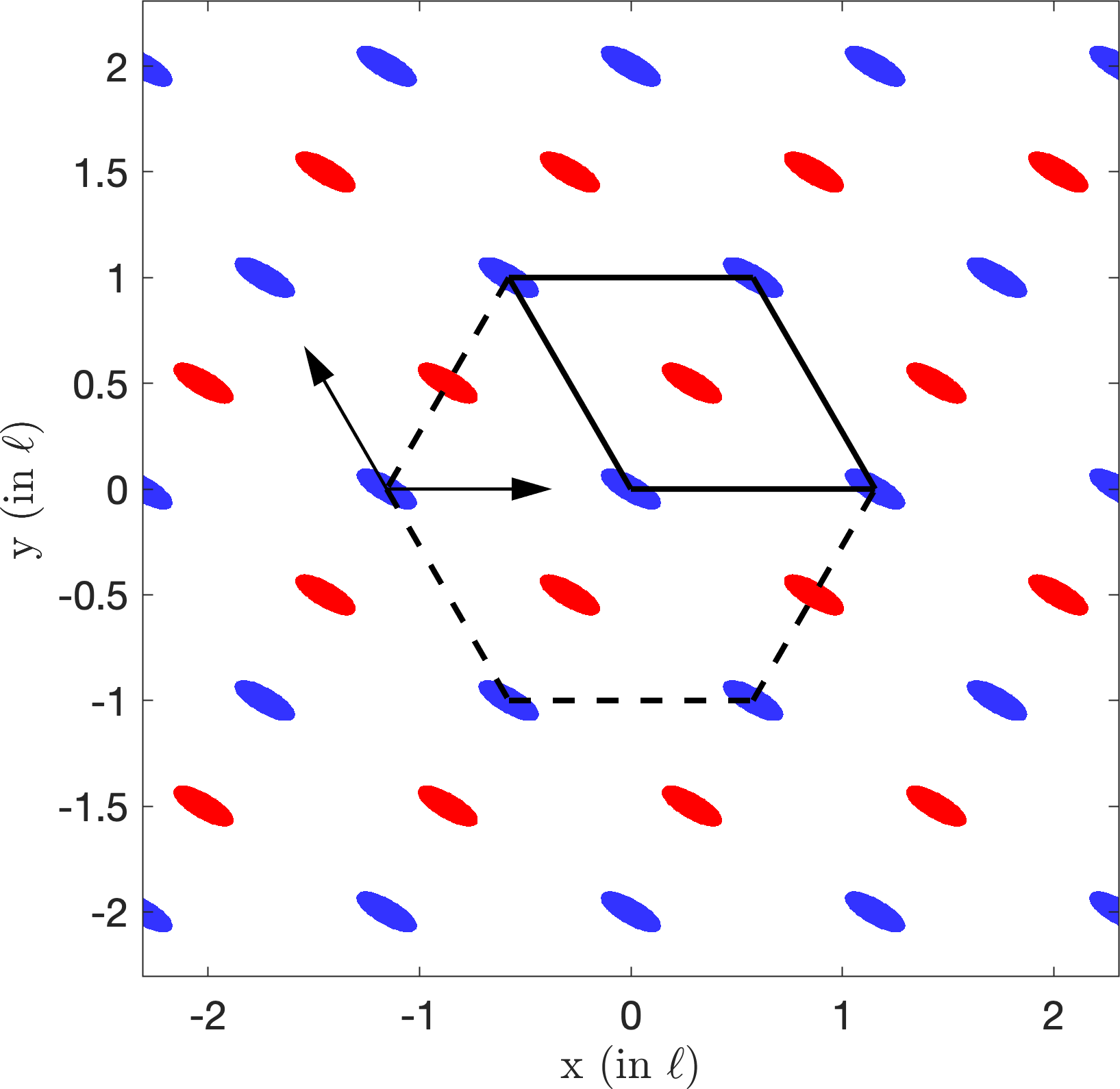
Later we looked at particle arrangements that are periodic¹⁸. An example of a periodic pattern is a chess board. It turns out one can achieve periodic patterns of particles using waves in two (three) dimensions using two (three) plane wave directions. The particle arrangements must be periodic (by construction) with a lattice that is the reciprocal of the wavevectors. Since we operate at a single frequency, the wavevectors are constrained to have the same length (wavenumber). Therefore the possible crystallographic symmetries that can be obtained via this method are limited. For example in two dimensions only Orthorhombic Centered, Hexagonal and Tetragonal symmetries are possible (out of 5 possible crystallographic symmetries). These symmetries look as follows:

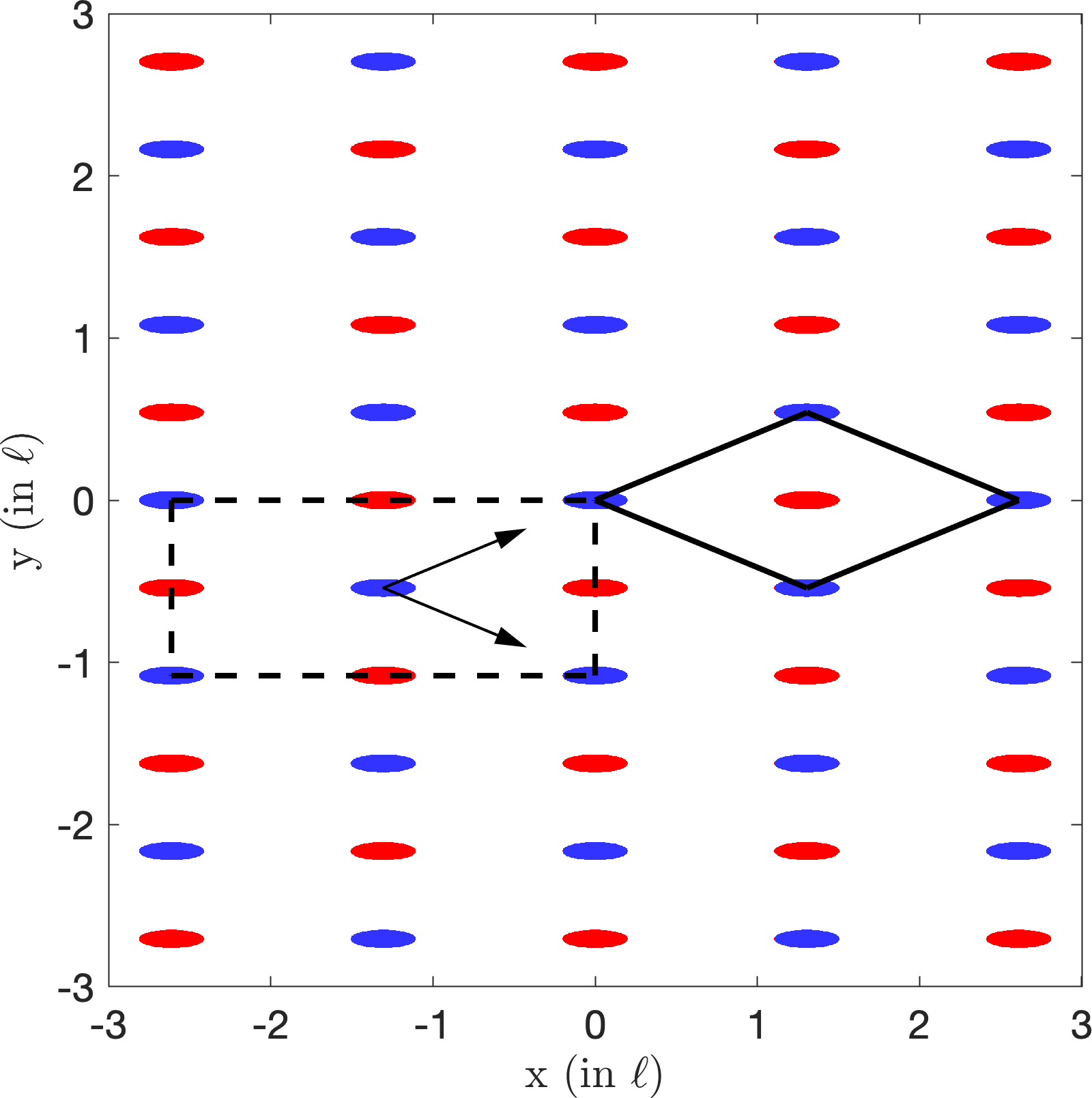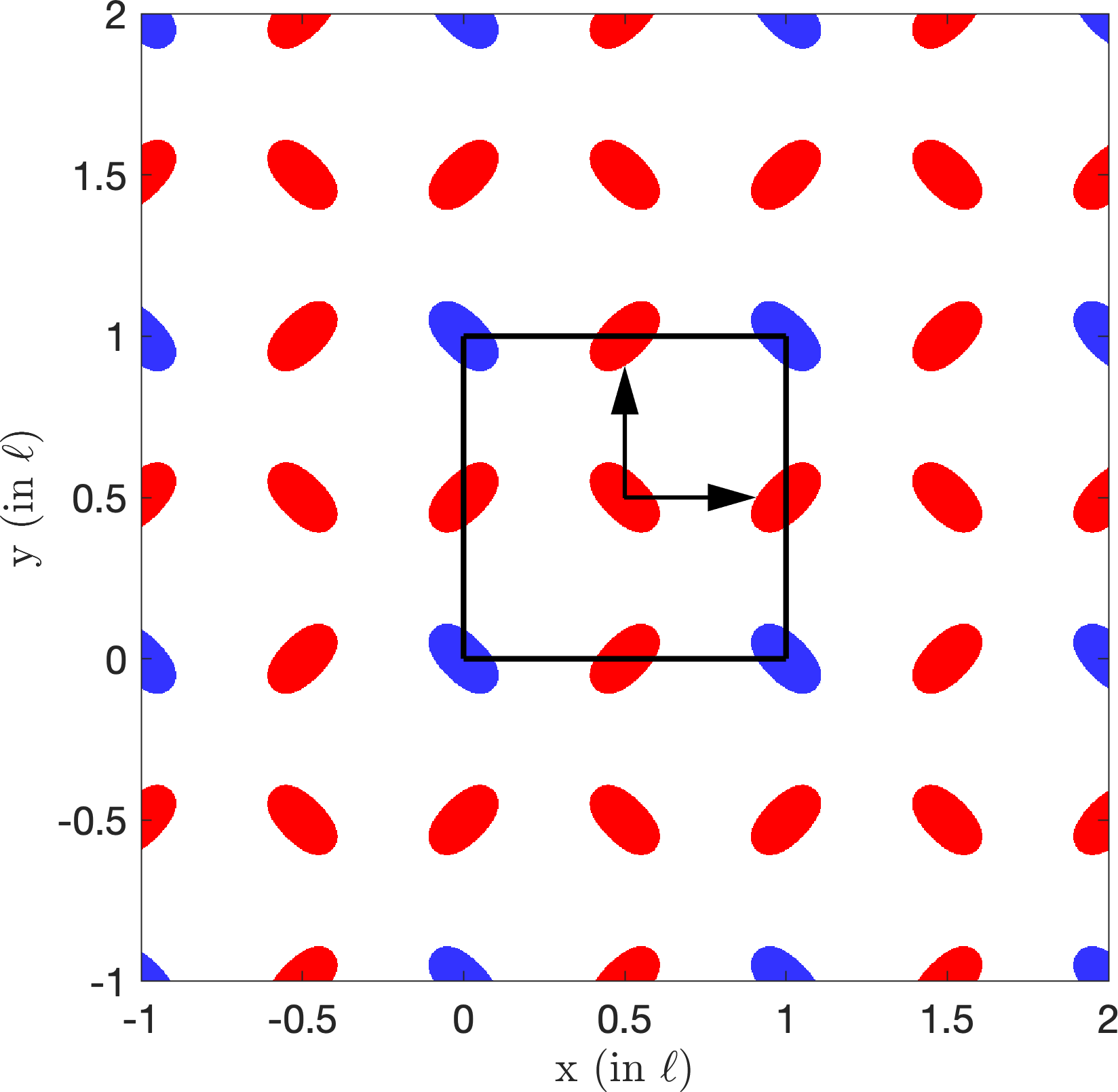Orthorhombic Centered	Hexagonal	Tetragonal

This begs the question, what happens if we have more plane wave directions than dimensions? In this case we get quasiperiodic particle arrangements¹⁹. These are mesmerizing (at least to me), here is an example of a pattern with a ten-fold symmetry (incidentally the same symmetry as the Penrose tiling).
Moreover we demonstrated¹⁹ that such patterns can also be achieved experimentally and that we get a reasonable agreement between the simulations and experiments.

Collaborators: I got into this problem in 2012 thanks to some very inquisitive questions posed to me by John Greenhall. John was at the time a Ph.D. student working under the supervision of Bart Raeymaekers (Mechanical Engineering, Virginia Tech formerly at the U. of Utah). He has moved on to Los Alamos National Laboraties. Since then I have had also the pleasure of working on this problem with other students from the Raeymaekers lab: Milo Prisbrey (now at Los Alamos National Laboratories), Soheyl Noparast and Tre Presley. On the mathematics side, my former Ph.D. student China Mauck (now at STV) worked on this problem and Elena Cherkaev (Mathematics, U of Utah) as well.