Sanghoon Kwak Wins U Graduate Research Fellowship
Sanghoon Kwak
Sanghoon Kwak, a third-year Ph.D. candidate in the Department of Mathematics, has been awarded a Graduate Research Fellowship (GRF) from the University of Utah. The purpose of the GRF is to provide graduate students with an opportunity to do full-time research during an academic year. Recipients are selected and evaluated on the quality and impact of their research or creative project, their achievements, and their potential for success.
“I am tremendously honored and humbled to receive a GRF,” said Kwak. “It’s a huge affirmation of the work I’ve done for the last three years and an encouraging nod to my future work. The fellowship will allow me to have more solid blocks of time to dedicate to my research. I also want to recognize the support, trust, and patience I’ve received from my advisors, Distinguished Professor Mladen Bestvina, and Assistant Professor Priyam Patel.”
Kwak studies geometric group theory, which is an area of mathematics devoted to studying groups, endowing them with a metric, and treating them as geometric objects. Geometric group theory is a relatively new area of mathematics, providing a variety of applications to geometry, topology, group theory, number theory and graph theory.Many junior researchers have been drawn to this field, and the Math Department at the university has one of the leading groups.
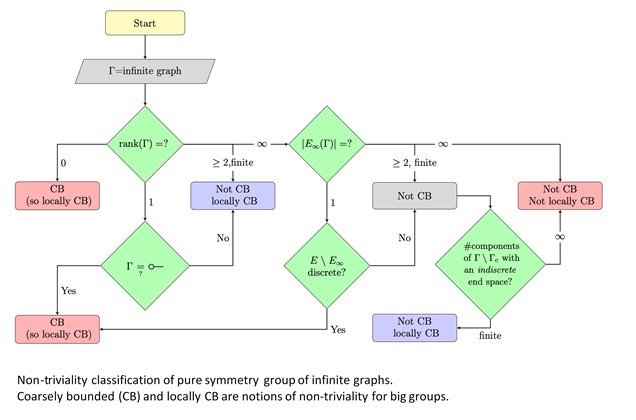
In his research, Kwak works on the group of symmetries of infinite graphs that correspond to infinite-type surfaces. In the fall of 2021, Dr. Bestvina and Dr. Yael Algom-Kfir, a lecturer at the University of Haifa in Israel who received her Ph.D. in mathematics from the U in 2010, conducted a pioneering study on the symmetry group of infinite-type graphs. Based on this study, Kwak and other colleagues in the Math Department were able to develop a complete classification, of which infinite-type graphs have symmetry groups with “interesting” geometry. The GRF will allow him to continue his work in this area.
Kwak has always enjoyed the beauty, simplicity, and universality of math. “One of
the things I like about mathematics, compared to the other sciences, is that mathematical
knowledge has no expiration date,” he said. “An established fact in mathematics, as
long as it is rigorously proved, rests forever. For me, publishing a paper is like
putting a small stone out there that will last. The stone could be a part of a cornerstone
of a castle to build on; it could be placed on top of a pyramid of stones; or it could
serve as a kind of Rosetta stone that unlocks understanding between different fields;
or it could contribute to a mosaic of stones that helps us understand a larger piece
of a picture.”
He received a bachelor’s degree in mathematics from the Korea Advanced Institute of Science and Technology (KAIST) in South Korea. During his undergraduate education, Dr. Bestvina visited KAIST and gave a lecture on geometric group theory. Kwak attended his presentation and wanted to learn more about the correspondence between surfaces and graphs. Following graduation, Kwak was accepted to the U for graduate school. After he receives his Ph.D., he hopes to continue his research and teach at a university.
Below is an example of Kwak’s work.
